CLein

posted September 6, 2011 by Stephan Brumme

What is CLein ?

CLein is a tiny, portable freeware program which displays all relevant information about the OpenCL drivers installed on your system.
It contains a small benchmark to compare the computing power of your host CPU and your OpenCL device(s), too.

If you have no idea what OpenCL is then read this article on Wikipedia.
See screenshots below to get a first impression of CLein.

The name CLein is based on the German word klein = small, little (now you know what that Calvin underwear really means ...)

Requirements

Windows XP, Vista or 7 (32 and 64 bits)
OpenCL driver (e.g. NVidia ForceWare 195.39+ or AMD/ATI Catalyst 9.12+, the Intel OpenCL SDK, ...)
No installation needed: just download clein.exe and start it
Nothing else: no need for .NET, runtime DLLs or anything else

Download

Git users: scroll down to the repository link

Download clein.exe

Latest release: September 7, 2011, size: 108.5 kBytes

CRC32: e34bf29b
MD5: 8d5500a852d203d5d1326ff0afa72f9e
SHA1: 1185354ebc249d8eed1597cc1300fce526bc3cf8
SHA256:ecb9e55bd907c36fcbe193d18224684f4b8464aaa4605ccfe2960bea97236bd1

Stay up-to-date:git clone https://create.stephan-brumme.com/clein/git

If you encounter any bugs/problems or have ideas for improving future versions, please write me an email: create@stephan-brumme.com

Changelog

version 0.2
- latest and greatest
- September 7, 2011
- fixed some GUI bugs
- increased ParallelLevel to 4 (≈10% faster)
version 0.1
- September 6, 2011
- initial release

Screenshots

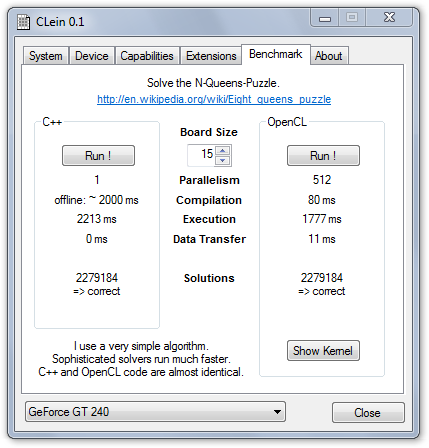
Technical Background

CLein is written in C++ - and obviously the Benchmark kernel is written in OpenCL ;-)

At work I almost exclusively use MFC, Qt and (rarely) .NET but the resulting executables are either excessively large and/or have tons of DLL dependencies. Therefore I decided to program CLein the old-fashioned way: just pure Win32 API. I statically link to the C/C++ runtime including STL's std::string and std::vector.

Even though CLein is freeware, its source code is currently not publicly available except for the simple OpenCL kernel of the Benchmark tab (see below or click Show Kernel). At the moment, OpenCL 1.1 is the most recent specification released by The Khronos Group. The Capabilities tab includes all features available in OpenCL 1.0 and 1.1. The kernel is compliant to OpenCL 1.0.

Several N-Queens solvers can be found online, including at least one based on OpenCL. They are fine-tuned for high performance at the cost of a high kernel complexity and/or extensive precomputations. CLein's kernel is short'n'simple and pretty much identical in C++ and OpenCL. The algorithm is based on backtracking and does not exploit board symmetries. Each thread's only input are the board size and its the thread ID (via get_global_id / get_global_size). Each thread stores the number of solutions in data[thread] which is summed by the host program in C++.

To make the kernel even simpler you can revert to a (slower) single-threaded solution: ParallelLevel should be set to 0 and lines 30-59 can be removed.

hide OpenCL Kernel


     // maximum board size
     #define MaxQueens 20
     // maximum degree of parallelism: ParallelLevel^queens, e.g. 4^8
     #define ParallelLevel 4
     
     kernel void myKernel(global int* write_only data, int queens)
     {
       const int thread = get_global_id(0);
       data[thread] = 0;
     
       // simple solutions if below ParallelLevel
       if (queens == 1)
         data[0] = 1;
       if (queens == 4)
         data[0] = 4;
       if (queens <= 4 || queens > MaxQueens)
         return;
     
       // all bits set
       const int fullMask = (1 << queens) - 1;
     
       local int leftStack [MaxQueens+1];
       local int rightStack[MaxQueens+1];
       local int downStack [MaxQueens+1];
       local int maskStack [MaxQueens+1];
       leftStack [0] = 0;
       rightStack[0] = 0;
       downStack [0] = 0;
       maskStack [0] = 0;
     
       int foundSolutions = 0;
     
       // spread work amongst cores
       int maxI = 1;
       for (int i = 0; i < ParallelLevel; i++)
         maxI *= queens;
       for (int i = thread; i < maxI; i += get_global_size(0))
       {
         int id = i;
         int level;
         bool invalid = false;
         for (level = 0; level < ParallelLevel; level++)
         {
           const int bitPos = 1 << (id % queens);
           id /= queens;
     
           // collides with another queens ?
           if ((bitPos & maskStack[level]) != 0)
           {
             invalid = true;
             break;
           }
     
           // place queen
           leftStack [level+1] = (leftStack [level] | bitPos) << 1;
           rightStack[level+1] = (rightStack[level] | bitPos) >> 1;
           downStack [level+1] =  downStack [level] | bitPos;
           maskStack [level+1] = leftStack[level+1] | rightStack[level+1] | downStack[level+1];
         }
         if (invalid)
           continue;
     
         // try to fill board with backtracking
         while (level >= ParallelLevel)
         {
           // lowest bit not set (see https://bits.stephan-brumme.com/lowestBitNotSet.html)
           const int freeSpot = (maskStack[level] + 1) & ~maskStack[level];
     
           // invalid ?
           if ((freeSpot & fullMask) == 0)
           {
             level--;
             continue;
           }
     
           // board completed ?
           if (level == queens-1)
           {
             foundSolutions++;
             level--;
             continue;
           }
     
           maskStack[level] |= freeSpot;
     
           // place queen and dig one level deeper
           level++;
           leftStack [level] = (leftStack [level-1] | freeSpot) << 1;
           downStack [level] =  downStack [level-1] | freeSpot;
           rightStack[level] = (rightStack[level-1] | freeSpot) >> 1;
           maskStack [level] = leftStack[level] | downStack[level] | rightStack[level];
         }
       }
     
       data[thread] = foundSolutions;
     }

Benchmark

These are the timings of my computers (Execution only):

Code	Device		Compiler	MHz	Cores	Threads	8x8	9x9	10x10	11x11	12x12	13x13	14x14	15x15
C++	CPU	Intel Core i7 860	Visual C++	2800MHz	4x2	1	1ms	1ms	2ms	4ms	18ms	74ms	362ms	2192ms
OpenCL	CPU	Intel Core i7 860	Intel OpenCL SDK 1.1	2800MHz	4x2	512	1ms	1ms	1ms	2ms	11ms	56ms	327ms	2036ms
OpenCL	CPU	Intel Core i7 860	AMD APP SDK 2	2800MHz	4x2	1024	1ms	1ms	1ms	3ms	14ms	71ms	415ms	2584ms
OpenCL	GPGPU	NVidia GT240	Driver 280.26	1462MHz	12x8	512	1ms	2ms	3ms	7ms	33ms	64ms	292ms	1562ms
						Solutions:	92	352	724	2680	14200	73712	365596	2279184
C++	CPU	Intel Pentium D 820	Visual C++	2666MHz	2	1	1ms	1ms	2ms	5ms	20ms	106ms	613ms	3962ms
OpenCL	GPGPU	NVidia 8600GT	Driver 280.26	1188MHz	4x8	512					37ms	177ms	1021ms	5925ms

Note: The timings for my Nvidia GT240 change significantly from run to run. Displayed are the best timings measured after 10 runs.

I increased ParallelLevel from 3 to 4 in version 0.2 which give a performance increase of about 10%.

As already stated in the paragraph above, there are many solvers that run much faster - but they are much more complex, too.


June 30, 2021: Length-Limited Prefix Codes April 13, 2020: smalLZ4 - optimal LZ4 compression June 17, 2019: toojpeg - a JPEG encoder in a single C++ file ... and 30 more !	RSS	www.stephan-brumme.com bits.stephan-brumme.com photos.stephan-brumme.com minime.stephan-brumme.com
© 2011-2024 Stephan Brumme products and company names mentioned may be trademarks of their respective owners. see my disclaimer. dude, this is the end ... of this page.